Fourier Transforms in VirtualLab Fusion

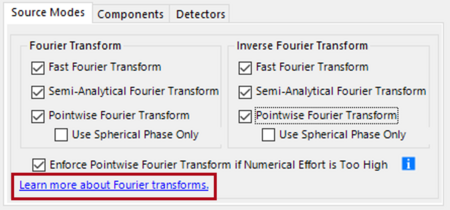
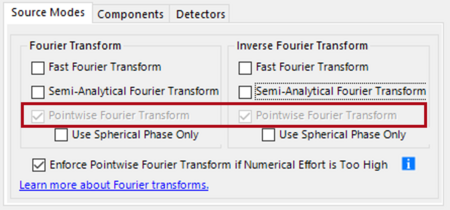
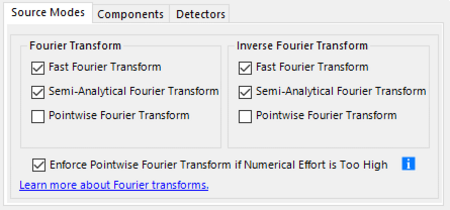
Figure 1 shows the dialogue for the settings of the Fourier transform which is accessible in components, detectors, system modeling settings, and global settings. Mathematically a Fourier transform forms an integral operator. Its input and output are complex-valued functions, which represent field components in physical-optics modeling. For the numerical implementation typically an equidistant sampling grid is used for both functions and the discrete Fourier transform is obtained. If we assume N sampling points in both domains, the discrete Fourier transform requires N² operations. Thanks to the Fast Fourier Transform (FFT) algorithm this numerical effort can be reduced to be proportional to N instead of N².  However, in optics modeling the number N can be exceedingly high, mainly because of the equidistant sampling of phase factors. We developed a semi-analytical Fourier transform (SFT)  to overcome that problem for moderate phase factors, by extracting a polynomial of second degree from the phase and dealing with it analytically [Wang2019].
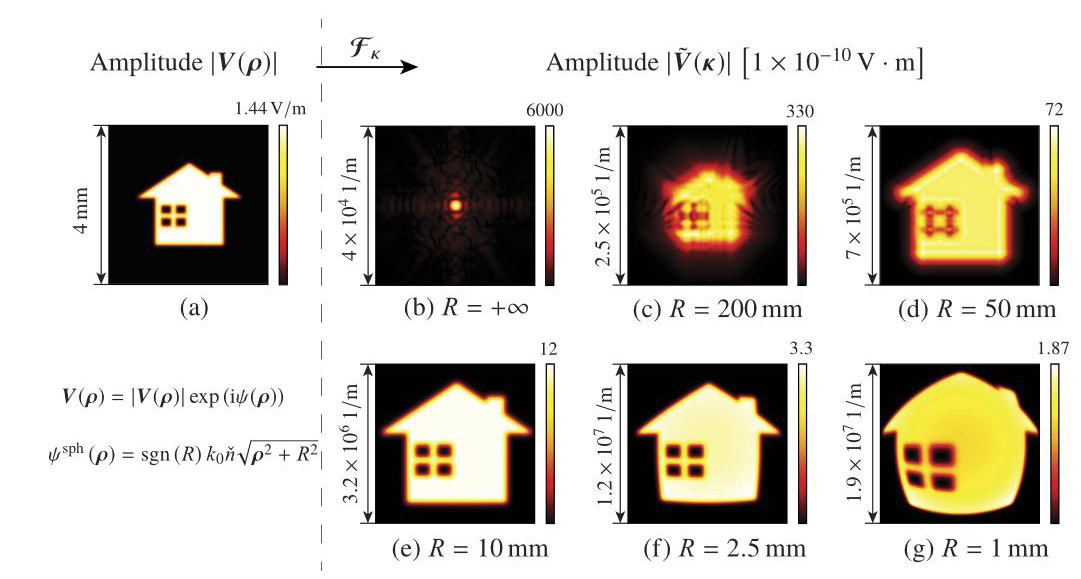
The SFT does not include any approximation, but benefits from a suitable reformulation of one FFT by two FFTs. For very weak wavefront phases, e.g., for a field in its focal region, the SFT can require higher numerical effort than the FFT. VirtualLab Fusion selects the best choice if both Fourier transforms are selected in the settings. For strong wavefront phases, that means high numerical aperture situations, the numerical effort for the SFT is high as well. Fortunately, we found that in this case the integral Fourier transform can be replaced by the approximate pointwise Fourier transform (PFT) which does not require an equidistant sampling of the phase factor but enables a direct sampling of the phase itself [Wang2019]. In VirtualLab Fusion we apply Zernike polynomials and spline interpolation for representing wavefront phases when applying the PFT [Badar2021]. It is combined with an equidistant sampling of the residual complex amplitude which leads to the general hybrid sampling concept in VirtualLab Fusion (see Field Tracing Accuracy Settings).

Next, we like to discuss the physical meaning of different settings in the Fourier transform dialogue. The propagation of electromagnetic fields in homogeneous media can be done component-wise without restriction of validity. In VirtualLab Fusion field information is always stored and processed vectorially and propagation is done per component.  

The Fourier transform dialogue comes with settings for the forward and the inverse Fourier transform. Together with the rigorous field propagation kernel in the k-domain, the Fourier transforms provide a rigorous propagation operator in space domain via the k-domain. It should be mentioned that the same operation can be completely formulated via convolution theorem in the space domain and the Rayleigh-Sommerfeld diffraction integral is obtained. This integral is another mathematically representation of the very same operator via the k-domain. The difference is in the numerical complexity, which is proportional to N via k-domain and proportional  to N² in space domain via the integral. Thus, in VirtualLab Fusion we work via k-domain.

It should be emphasized, that all propagation techniques in VirtualLab Fusion enables the propagation between parallel planes as well as tilted planes without reducing the calculation speed [Zhang2016].

We distinguish between the settings for the source mode propagation into the system, the propagation between components, and the propagation to detectors. This can be conveniently done via the modeling levels (see Seamless Transition from Ray to Physical Optics) or directly via the settings.

In VirtualLab Fusion we do not apply a paraxial or scalar modeling approximation. Thus, the rigorous propagation kernel in k-domain is always applied per component and different propagation are controlled via the Fourier transforms only. This is discussed next.

Fully Automatic Mode  

Figure 1 shows the setting for which VirtualLab Fusion automatically selects FFT and SFT based on numerical effort estimations and the PFT when the approximation of the pointwise approach is justified (see Field Tracing Accuracy Settings). The option  Enforce Pointwise Fourier Transform if Numerical Effort is Too High disregards the accuracy of the PFT and applies it, if the FFT and the SFT require too high numerical effort. The threshold for acceptable numerical effort is set in Global Options|Performance|Ram Consumption.

The fully automatic mode includes all the special cases which are considered in what follows.  

Spectrum of Plane Wave Operator and Rayleigh-Sommerfeld Integral

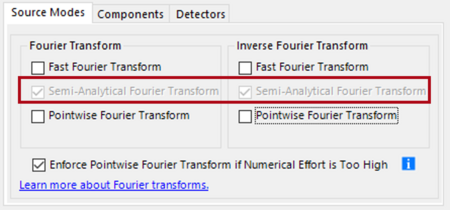
Figure 2 shows the settings for implementing the Spectrum of Plane Wave (SPW) operator in VirtualLab Fusion. The additional selection of the SFT does not change the physics but improves the numerical efficiency of the operation. The inclusion of tilted planes generalizes the SPW operator in VirtualLab Fusion further.

As mentioned before, the SPW operator and the Rayleigh-Sommerfeld integral are different mathematical expressions of the same physical solution. It should be mentioned that the Huygens’s integral is an approximated version of the Rayleigh-Sommerfeld integral. It does not model the field close (some wavelengths) to the initial plane correctly since one term in the Rayleigh-Sommerfeld integral is neglected. The SPW operator is rigorous and accurate for any propagation distance. The inclusion of the SFT makes the SPW operator in VirtualLab Fusion numerically efficient and fast.

The Fresnel integral follows from the SPW operator by a paraxial approximation of the propagation kernel. That enables the analytical treatment of a quadratic phase factor which makes the Fresnel integral attractive because of reduced numerical effort compared to the SPW operator. However, in VirtualLab Fusion we do not use a paraxial approximation but benefit from the semi-analytical Fourier transform (SFT) technique, which also allows the analytical treatment of a polynomial of second degree. Thus, the setting in Fig. 3 provides the same advantages as the Fresnel integral without the restriction to a paraxial case.

In literature you may find an argument, which states that the Fresnel propagation is not valid in near field or in far field. The truth is, that the Fresnel integral is valid for any propagation distance if the field is paraxial.

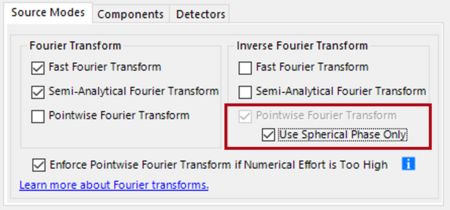
The far field integral is a powerful technique to propagate a field out of a focus or its waist into its far field zone. Mathematically the far field integral is obtained by selecting the pointwise Fourier transform in the inverse step of the SPW operator [Wang2021]. The well-known conventional far field integral uses in addition the condition, that just the spherical part of the wavefront phase is used for the inverse PFT. This case is shown in Fig. 4 with the selected Use Spherical Phase Only option. This option should be used when different integrals are to be compared. Usually, the option is unselected, and the generalized far field integral is applied in VirtualLab Fusion [Wang2021]. It should be mentioned that the far field integral includes the Fraunhofer integral if the field is paraxial.

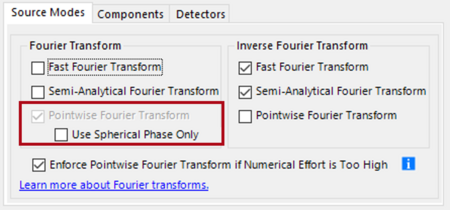
The generalized Debye integral follows, if the first Fourier transfrom is chosen to be pointwise as shown in Fig. 5 [Wang2020]. It is of paricular importance for the propagation of fields from the exit pupil or any other plane behind a lens system into the focal region. It requires a strong wavefront phase that means at least a moderate numerical aperture. The generalized Debye integral can also deal with stronger aberrations, whereas the conventional Debye integral is more restricted in this context. The option Use Spherical Phase Only enables the explicit use of the conventional Debye integral.

The conventional Debye integral is often used in ray tracing software to calculate the PSF/MTF in lens systems from the wavefront phase in the exit pupil. Sometimes that is referred to FFT technique because of the final inverse FFT. In VirtualLab Fusion we follow a much more  general approach in PSF/MTF calculation by using the most accurate combination of Fourier transforms in the general propagation concept. By that VirtualLab Fusion has no limitations with respect to numerical aperture, tilted planes, propagation distances, and amount of aberrations. In addition, modeling in VirtualLab Fusion includes all vectorial and polarization effects. All that comes with a fast propagation algorithm which is provided in a fully automatic mode of operation.  

The propagation through a focus or inside the far field are examples for the use of two pointwise Fourier transforms as indicated in Fig. 6. It leads to a particularly fast pointwise physical-optics propagation in the space domain [Baladron-Zorita2019].

Mathematically the pointwise propagation is expressed by a mapping of the input sampling values with the ones in the output plane.  Such a mapping can be expressed by a ray tracing step which leads to the connection of physical optics with ray optics. VirtualLab Fusion includes ray optics by the control of the Fourier transforms and by that a seamless transition between ray and physical optics is provided (see also Seamless Transition from Ray to Physical Optics).