Incorporate Diffraction
Where Necessary
To trace electromagnetic fields among components, a model simulating field propagation through homogeneous and isotropic media;
such as vacuum, air, glass, and water – is essential. This process is termed free-space propagation.
Diffraction Becomes Apparent as Light Moves Through Free Space
Let us consider that we possess information about an electromagnetic field at the output of a certain source or from a component simulation model. Field tracing necessitates determining its propagation to further elements within its accessible range in a three-dimensional setup. The degree of diffraction observed when an electromagnetic field propagates through free space is contingent upon the specific characteristics of the field.
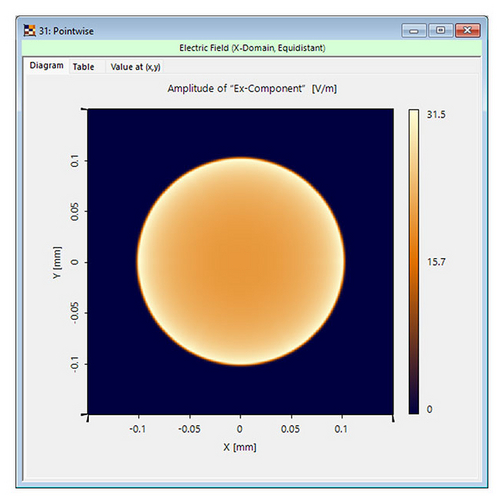
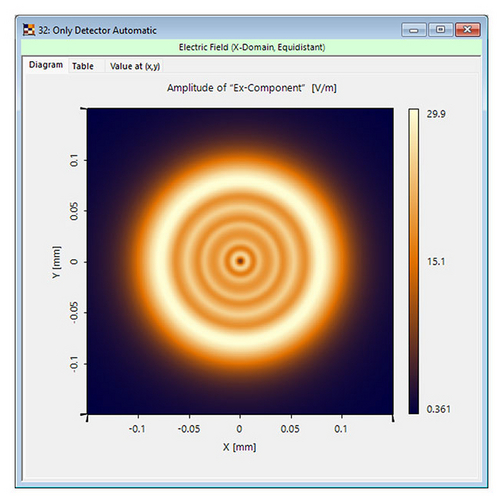
Geometric Propagation and Diffraction Integrals Required
When diffraction effects are minor, they may be ignored, allowing for the use of a geometrical model. In all other cases, it is vital to factor in diffraction effects by choosing the right diffraction integrals, such as the Rayleigh-Sommerfeld, Debye, and far-field integrals, to act as simulation models.
Ingenious Method for Effortless Incorporation of Diffraction Phenomena
The development team at VirtualLab Fusion has equipped the software with a cutting-edge free-space propagation technique. It facilitates a smooth switch between geometric models and any model that incorporates diffraction. Users have the option to either manually control the switching or let VirtualLab Fusion’s algorithms fully manage the decision of where to integrate diffraction into system modeling.
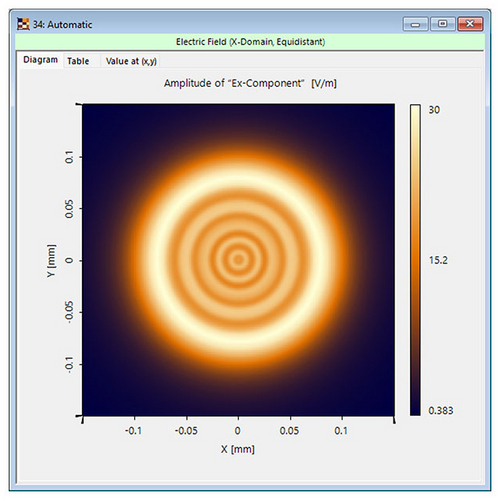
Wondering whether you need geometric or wave optics simulation?
No worries – VirtualLab Fusion evaluates your system and seamlessly toggles between both models as needed.
Ray Tracing Derives from Specific Configuration of Simulation Model
Upon request, opting for the manual method lets you skip diffraction entirely, relying only on a geometric simulation model. A ray-tracing simulation is what this scenario essentially results in.