Limitations of the FMM
The Fourier Modal Method (FMM), also known as Rigorous Coupled Wave Analysis (RCWA), is an eigenmode solver in the spatial frequency domain (k domain) used among others in the Grating component. It models field propagation by dividing the structure into multiple layers with periodic boundary conditions. For detailed mathematical insights, refer to this: FMM / RCWA [S-Martix]
Limitations of FMM/RCWA
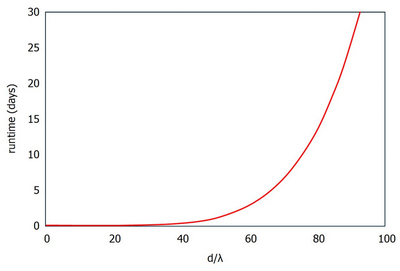
The computational complexity of the operator scales at least with \( k \cdot L^{2.807} \) where \( k \) is the number of layers, and \( L = L_{\mathrm{prop}} + L_{\mathrm{eva}} \) is the total number of modes, combining propagating and evanescent modes. In this chapter we are under the assumption that \( k \) and \( L_{\mathrm{eva}} \) have fixed values as they depend on the structure in mind and its corresponding material. Hence, in general they cannot be predicted analytically. They will be discussed in the next chapter in detail.
In 1D (lamellar) structures, the number of propagating modes increases linearly with the ratio of period to wavelength. This is due to the condition that a mode propagates only if \( k_z = \sqrt{k_0^2 - k_x^2} \) results in a real value. For lamellar (in e.g. x) gratings, we know:
\[ k_x = \frac{2\pi n}{d} \] \[ k_0 = \frac{2\pi}{\lambda} \]
where \( n \) is the number of diffraction orders, \( d \) the period and \( \lambda \) the wavelength. Fulfilling \( k_x^2 < k_0^2 \) then leads to an upper threshold for the maximum diffraction order:
\[ n < \frac{d}{\lambda} \]
Including all negative, positive and the zeroth order this results in \( L_{\mathrm{prop}} = (2n+1) \) propagation modes. For the 2D case similar considerations lead to
\[ n < \frac{d_x}{\lambda}, \quad m < \frac{d_y}{\lambda} \]
with \( n,m \) being the diffraction orders in x and y and \( L_{\mathrm{prop}} = (2n+1) \cdot (2m+1) \) respectively.
In Figure 1 this dependency on the example of a 2D quadratic grating (\( d_x = d_y \)) is visualized.
Convergence of the FMM/RCWA
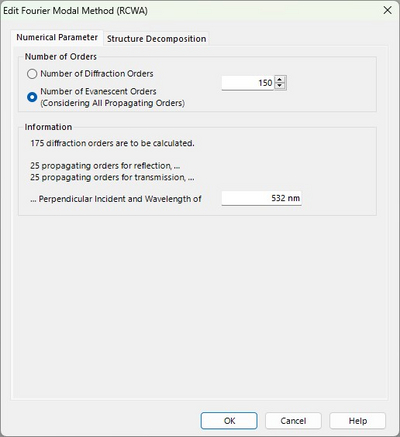
In the Numerical Parameters tab, users can define the number of orders considered by the FMM/RCWA solver, either by specifying the diffraction orders directly or by setting the number of evanescent orders to include. We recommend the latter option as it automatically accounts for all propagating orders plus the specified evanescent orders.
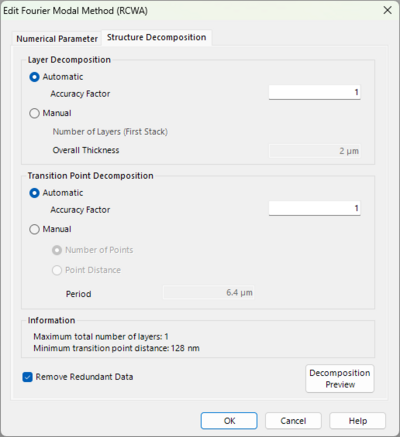
The solver always functions on a discretized structure. Hence, the Structure Decomposition tab controls the sampling parameters of the discretization using Transition Points (X, Y) and Layers (Z). A preview is available to visualize the current discretization.
For structures consisting out of dielectric materials the automatic settings typically are sufficient. For certain scenarios however, such as metal surfaces that require more evanescent orders or meta-structure which are notorious for their small feature sizes, manual adjustments may be necessary. We suggest always testing the convergence of the FMM/RCWA solver by first fixing the number of orders and refining the discretization. Once stable results are achieved, increase the number of orders (e.g., via a Parameter Run) until convergence is reached.