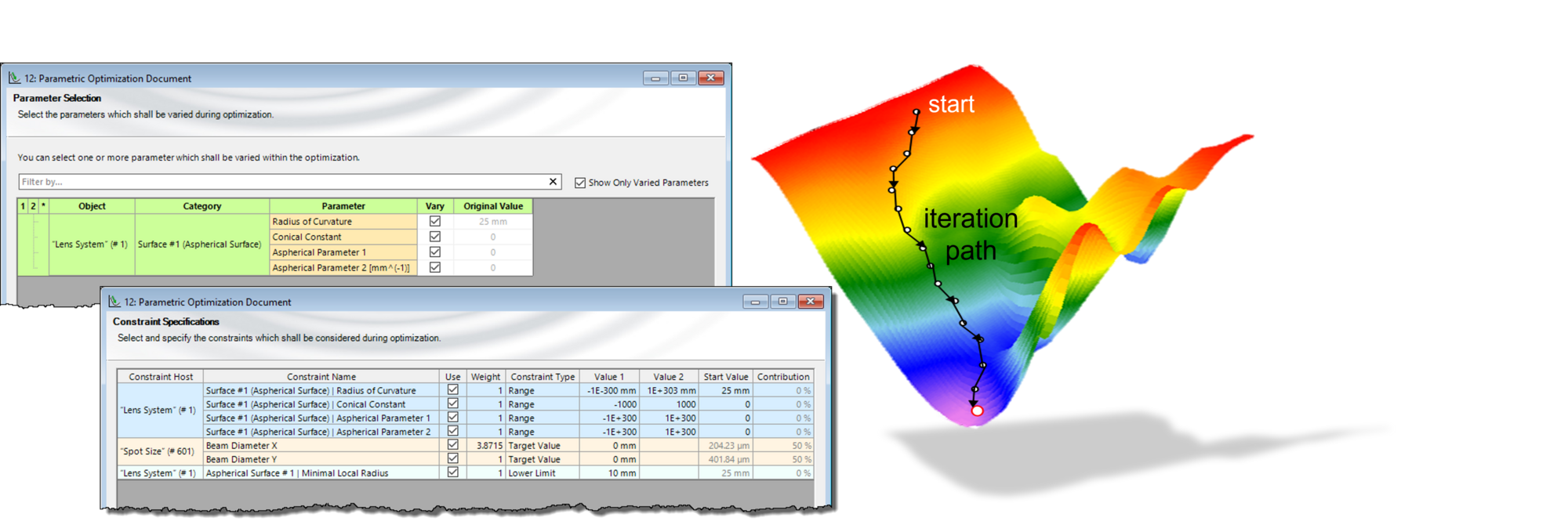
Notes on Constraints

Optimization of given constraints

The goal of a parametric optimization is to fulfill a set of given constraints as good as possible. To this end a target function value T is calculated for each simulation step which is then minimized by changing the constraint values:

T = Σ w_i · T_i

T_i is the contribution of the constraint i (see below) and w_i is the Weight you can set in the Constraint Specifications table.

The main idea is that a contribution function T_i is zero if the constraint is fulfilled and becoming larger the more we depart from the desired values.

There are four possible definitions of the contribution functions T_i :

Lower limit: The value v of the parameter should be larger or equal than the given lower limit v_min.

$Lower limit formula$

Upper limit: The value v of the parameter should be smaller or equal than the given upper limit v_max.

$Upper limit formula$

Range: The value v of the parameter should be in the range v_min ≤ v ≤ v_max.

$Range formula$

Target value: The value v of the parameter should be exactly the target value v_t , which can be infinity.

$Target value formula$

Independently from the formulas given above, there might be the case that the Optical Setup cannot be calculated for the current values of the constraints. For example, the wavelength to be optimized might be out of the range of all involved materials or a division by zero might occur. In such a case, the target function is always the largest possible number, shown as “NaN” in the result table.

Consequences for good optimization results

As the contribution function is zero if the constraint is fulfilled, too generous constraints which are easily fulfilled don’t have a large effect. For example, if your requirement is that the spot size is at least less than 1 mm, you might use an upper limit of 1 mm. But then you might end up with a spot size of 0.999 mm which might not be optimal. Better to make the constraint less generous by setting an upper limit of e.g. 1 µm. Then the spot size is made as small as possible.

Constraints which are almost fulfilled only have a small contribution function. Thus, in rare cases the optimal result might be one where constraints are a bit violated. This could be solved by introducing “hard” constraints (T_i = 0 if fulfilled, T_i = ∞ if violated). But it turned out that such hard constraints yield worse optimization results.

Steps with violated constraints are not shown by default. You can change this by unchecking Show Only Valid Simulation Steps in the Property Grid.